This comprehensive guide offers a wide range of algebra questions and answers in PDF format, providing detailed solutions suitable for learners of all levels, enhancing problem-solving skills effectively.
1.1 Importance of Algebra in Mathematics
Algebra is a cornerstone of mathematics, serving as a fundamental tool for problem-solving and critical thinking. It introduces variables, equations, and functions, which are essential for understanding more advanced mathematical concepts. Mastering algebraic principles enhances logical reasoning and analytical skills, benefiting students in various academic and real-world applications. Its applications span across science, technology, engineering, and mathematics (STEM) fields, making it indispensable for careers in these areas. Algebra also builds a strong foundation for higher-level mathematics, ensuring students are well-prepared for future challenges. By fostering a deep understanding of algebra, learners develop the ability to approach complex problems systematically, a skill valued in both academic and professional settings. The importance of algebra lies in its universal applicability and its role in shaping a robust mathematical mindset.
1.2 Benefits of Using PDF Resources for Algebra
Using PDF resources for algebra offers numerous advantages for learners. These resources are accessible anytime, allowing students to study at their own pace without requiring an internet connection; PDFs are often well-organized, making it easy to navigate through topics, examples, and solutions. They can be annotated and highlighted, enabling active learning and quick reference. Additionally, PDF resources are portable, meaning students can carry multiple algebra guides on a single device. Many PDF resources are free or low-cost, making quality algebra education accessible to everyone. They also reduce the need for physical textbooks, promoting environmental sustainability. Furthermore, PDFs can be shared easily among peers and educators, fostering collaborative learning. Overall, PDF resources provide a flexible, efficient, and cost-effective way to master algebra, catering to diverse learning styles and preferences.

Basic Algebra Questions and Answers
This section covers essential algebra topics with sample questions for beginners, detailed solutions, and practical tips to avoid common mistakes, helping learners build a strong foundation.
2.1 Sample Questions for Beginners
Start your algebra journey with these beginner-friendly questions, such as solving for x in linear equations, simplifying expressions, and understanding variables. Perfect for building confidence and foundational skills.
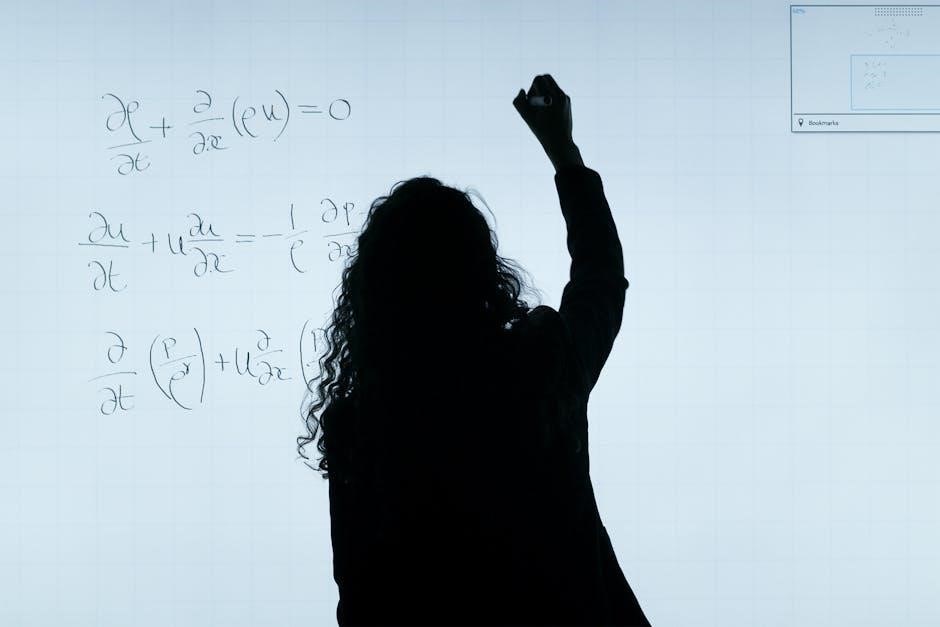
2.2 Detailed Solutions to Common Problems
Master basic algebra with step-by-step solutions to frequently encountered problems. Each solution breaks down complex equations into manageable parts, ensuring a clear understanding of every concept and method. This approach helps learners grasp the logic behind each step, making problem-solving more intuitive and effective. By following these detailed explanations, students can identify common mistakes and develop strategies to avoid them, fostering a stronger foundation in algebra. These solutions are ideal for self-study or classroom use, providing a comprehensive learning experience that builds confidence and proficiency in tackling algebraic challenges.
2.3 Avoiding Mistakes in Basic Algebra
Common algebraic errors often stem from improper sign handling, incorrect factoring, or misapplying rules. To avoid these, always double-check each step, especially when dealing with negative numbers or distributing terms. Mismanagement of fractions and exponents can also lead to mistakes, so ensure proper simplification before solving. Another pitfall is rushing through problems without reviewing work. Taking time to verify each operation can significantly reduce errors. Additionally, understanding the underlying concepts rather than memorizing formulas helps prevent mistakes. Using online tools like Mathway or Brainly to verify solutions can reinforce learning and highlight areas needing improvement. By adopting a systematic approach and practicing regularly, students can minimize errors and build a strong algebraic foundation. Remember, precision and patience are key to mastering basic algebra effectively.

Intermediate Algebra Questions and Answers
This section provides a comprehensive collection of intermediate algebra questions and answers, covering quadratic equations, polynomial expressions, and systems of equations to enhance problem-solving skills effectively.
3.1 Solving Quadratic Equations
Solving quadratic equations is a fundamental skill in intermediate algebra, involving equations of the form ( ax^2 + bx + c = 0 ). This section provides detailed solutions and methods, such as factoring, completing the square, and applying the quadratic formula. Practice questions and answers are included to help learners master these techniques. Multiple-choice questions and step-by-step explanations ensure a thorough understanding of quadratic equations. Common mistakes and tips for avoiding errors are also highlighted, making this resource invaluable for students seeking to improve their problem-solving abilities. By working through these examples, learners can confidently tackle quadratic equations in various mathematical contexts.
3.2 Simplifying Algebraic Expressions
Simplifying algebraic expressions is a core intermediate algebra skill, focusing on combining like terms, applying distributive properties, and factoring. This section provides clear examples, practice questions, and detailed answers to help learners master these techniques. Common expressions involve variables, constants, and coefficients, with step-by-step solutions guiding students through the process. Tips are included to avoid errors, such as misapplying signs or misunderstanding order of operations. Multiple-choice questions and word problems enhance understanding, while solutions highlight key steps for clarity. By practicing these problems, students can improve their ability to simplify complex expressions efficiently, a crucial skill for advancing in algebra and related math subjects.
3.3 Strategies for Problem-Solving
Mastering problem-solving in algebra requires a systematic approach and effective strategies. Start by understanding the problem fully, identifying what is given and what needs to be found. Break down complex problems into smaller, manageable steps, and use known formulas or properties to simplify. Common techniques include factoring, substitution, and elimination. Practice reverse thinking by working backward from the solution to the problem. Additionally, leveraging visual aids like graphs or tables can enhance understanding. Regular review of mistakes helps identify patterns and improve accuracy. Developing a growth mindset and persisting through challenges are key to success. These strategies, combined with consistent practice, equip learners with the tools to tackle even the most daunting algebra problems confidently and effectively.
College Algebra Questions and Answers
This section offers a collection of college algebra questions and answers, providing detailed solutions to multiple-choice and word problems, helping students master advanced algebraic concepts and prepare for exams.
4.1 Multiple-Choice Questions
Multiple-choice questions are an essential part of college algebra exams, offering a structured approach to testing knowledge. These questions cover a wide range of topics, from solving quadratic equations to simplifying algebraic expressions. They are designed to assess problem-solving skills, conceptual understanding, and the ability to apply algebraic principles to real-world problems. Many resources, including PDF guides, provide practice sets of multiple-choice questions with detailed solutions, helping students identify areas for improvement. Time management is crucial, as these questions often require quick and accurate responses. Strategies such as eliminating incorrect options and understanding common algebraic structures can significantly improve performance. Regular practice with these questions helps build confidence and ensures readiness for exams. They are a valuable tool for mastering college algebra and preparing for higher-level mathematics.
4.2 Word Problems in College Algebra
Word problems in college algebra are designed to apply algebraic concepts to real-world scenarios, enhancing problem-solving skills. These problems often involve translating descriptive situations into mathematical equations. Common topics include finance, physics, and mixing solutions, requiring students to identify variables and set up appropriate equations. A strong understanding of algebraic principles is essential for interpreting and solving these problems accurately. Many PDF resources offer practice exercises with detailed solutions, helping students improve their ability to tackle word problems effectively. Mastering these problems is crucial for success in college algebra and prepares students for advanced mathematics. Regular practice and reviewing solutions are recommended to build confidence and proficiency in this area.
4.3 Step-by-Step Solutions
Step-by-step solutions are invaluable for understanding complex algebra problems, breaking them down into manageable parts. These detailed explanations guide learners through each phase of problem-solving, from setting up equations to interpreting results. By following these structured solutions, students can identify common pitfalls and grasp underlying concepts more effectively. Many algebra PDF resources include step-by-step solutions for practice problems, enabling users to verify their work and improve accuracy. Educators often recommend these resources for self-study or homework help. The clarity and precision of step-by-step solutions make them an essential tool for mastering college algebra. They also serve as a reference for teachers preparing lessons or tutoring sessions. With consistent practice using these solutions, students build confidence and develop a deeper understanding of algebraic principles.

Resources for Algebra Questions and Answers
Discover various resources offering algebra questions and answers in PDF format, including interactive tools, detailed guides, and online platforms designed to enhance learning and problem-solving skills effectively.
5.1 Free Online PDF Guides
Free online PDF guides are an excellent resource for mastering algebra, offering a wealth of questions and answers tailored to various skill levels. These guides provide detailed step-by-step solutions, making complex problems easier to understand. Many PDF resources cover topics such as quadratic equations, algebraic expressions, and word problems, ensuring comprehensive coverage. They are ideal for self-study, homework help, or exam preparation. With their convenience and accessibility, these guides allow learners to practice anytime, anywhere, fostering a deeper understanding of algebraic concepts. Additionally, they often include multiple-choice questions, sample problems, and practice worksheets, catering to different learning styles. By utilizing these free resources, students can enhance their problem-solving skills and build confidence in tackling algebraic challenges effectively.
5.2 Mathway: A Problem Solver Tool
Mathway is a powerful online tool designed to help students solve algebra problems step-by-step. It supports a wide range of algebra topics, from basic equations to complex quadratic expressions. Users can input their problems, and Mathway provides detailed solutions, breaking down each step for better understanding. The tool is especially useful for visual learners, as it offers graphing capabilities and multiple viewing options. Mathway is accessible both online and through a mobile app, making it a versatile resource for homework help or exam preparation. While it complements PDF guides, Mathway’s interactive nature allows students to explore problems dynamically, enhancing their grasp of algebraic concepts. Its user-friendly interface and comprehensive coverage make it an invaluable asset for learners seeking to master algebra effectively.

5.3 Brainly for Homework Help
Brainly is a free online learning platform where students can ask homework questions and receive answers from a community of peers and experts. It is particularly useful for algebra, as users can post specific problems and receive detailed, step-by-step solutions. The platform fosters a collaborative environment, allowing students to engage with others, clarify doubts, and learn from one another. Brainly supports various learning styles, providing explanations in multiple formats to cater to different preferences. Its accessibility on both desktop and mobile apps makes it a convenient resource for algebra help anytime, anywhere. By leveraging Brainly, students can gain confidence in their problem-solving abilities and deepen their understanding of algebraic concepts, making it an excellent supplement to traditional study materials like PDF guides.
Study Tips for Mastering Algebra
Consistently practicing algebra, using visual aids like graphs, and staying organized helps build a strong foundation, improves problem-solving skills, and enhances conceptual understanding effectively over time.
6.1 Best Practices for Effective Learning

Mastering algebra requires consistent practice and a structured approach. Start by dedicating specific times daily to solve algebra questions, breaking sessions into manageable parts to avoid overwhelm. Use visual aids like graphs and diagrams to better understand abstract concepts. Regularly review mistakes to identify patterns and improve problem-solving strategies. Seek assistance from online tools such as Mathway or Brainly for step-by-step solutions and explanations. Incorporate flashcards for memorizing formulas and key terms. Engage in active learning by teaching concepts to others or explaining them aloud. Utilize practice worksheets and quizzes to reinforce understanding. Stay organized by maintaining a notebook of solved problems for quick revision. Lastly, adopt a growth mindset, embracing challenges as opportunities to learn and grow. By combining these strategies, learners can build a strong foundation in algebra and achieve long-term success.
6.2 Time Management During Exams
Effective time management is crucial during algebra exams to ensure all questions are attempted. Begin by quickly skimming through the entire paper to gauge the difficulty and allocate time accordingly. Allocate 70% of your time to easy and medium questions and 30% to challenging ones. Avoid spending too long on a single problem; move forward and return if time permits. Use the process of elimination for multiple-choice questions to increase accuracy. Always attempt to answer, even if unsure, as guessing can yield partial marks. After completing the paper, use remaining time to review your answers, checking for calculation errors or misread questions. Prioritize accuracy over speed, but maintain a steady pace to cover all sections. Proper time management reduces stress and maximizes your potential to score well.
6.3 Utilizing Practice Worksheets
Practice worksheets are invaluable tools for mastering algebra, offering a structured approach to learning and reinforcing key concepts. They provide a variety of problems, from basic to advanced, allowing learners to gradually build their skills. Consistent practice helps develop problem-solving strategies and improves speed and accuracy. Start with worksheets focusing on specific topics, such as solving equations or simplifying expressions, and progress to mixed-topic sheets to simulate exam conditions. Reviewing mistakes and understanding the reasoning behind correct answers is equally important. Setting aside dedicated time each day to complete worksheets ensures steady progress. Track your improvement over time and adjust your focus areas based on performance. Regular practice not only strengthens algebraic fluency but also boosts confidence, making complex problems more approachable. Incorporate these resources into your study routine for consistent growth and mastery of algebra.

The Role of Algebra in STEM Education
Algebra serves as a foundational skill in STEM fields, enhancing critical thinking and problem-solving abilities. It prepares students for advanced mathematics and its practical applications in science, technology, and engineering.
7.1 Enhancing Critical Thinking Skills
Algebra plays a pivotal role in developing critical thinking skills by encouraging analytical reasoning and systematic problem-solving. Solving algebraic equations requires breaking down complex problems into manageable parts, fostering logical reasoning and precision. These skills are essential in STEM fields, where complex challenges demand innovative solutions. Regular practice with algebra questions and answers helps students refine their ability to approach problems methodically, ensuring accuracy and efficiency. Over time, this process strengthens mental agility and sharpens the mind, preparing learners for advanced mathematical and scientific concepts. By mastering algebraic principles, students build a robust foundation for tackling real-world applications, from engineering to data analysis. Thus, algebra serves as a cornerstone for nurturing critical thinking, a skill vital for success in both academic and professional realms.
7.2 Preparing for Advanced Mathematics
Algebra serves as a foundational pillar for advancing into higher-level mathematics, equipping students with essential skills in manipulating variables, understanding functions, and solving complex equations. Mastery of algebraic principles enables learners to tackle advanced subjects like calculus, linear algebra, and differential equations with confidence. By fostering problem-solving abilities through algebraic reasoning, students develop the capacity to approach intricate mathematical challenges systematically. Regular practice with algebra questions and answers reinforces logical reasoning and analytical thinking, which are critical for grasping abstract concepts in advanced mathematics. Moreover, algebraic problem-solving cultivates a deep understanding of mathematical relationships, preparing students for the rigor of higher-level coursework. This strong foundation ensures that learners are well-equipped to excel in STEM disciplines and other fields requiring advanced mathematical proficiency.