Algebra 1 Notes PDF: A Comprehensive Study Plan
Effective Algebra 1 learning isn’t about rote memorization; it’s about understanding concepts deeply, like truly knowing a friend, not just their details.
Understanding the Importance of Conceptual Learning
Conceptual understanding in Algebra 1 transcends simply memorizing formulas. It’s about grasping the why behind the mathematical rules. Think of learning a person – you wouldn’t truly know them by just listing facts, but by experiencing shared activities. Similarly, understanding why the distributive property, X(YZ) = XY + XZ, works, and how it connects to combining like terms and FOIL, is crucial.
This deeper comprehension fosters problem-solving skills and adaptability. When faced with unfamiliar problems, students who understand the underlying concepts can apply their knowledge creatively, rather than relying on rigid memorization. A strong conceptual foundation allows for better retention and a more intuitive grasp of future mathematical topics. It’s about building a network of interconnected ideas, not isolated facts.
Ultimately, focusing on understanding transforms Algebra 1 from a collection of rules into a logical and empowering system.
The Pitfalls of Memorization in Algebra
Relying solely on memorization in Algebra 1 is a surprisingly effective path to struggling. While quickly recalling formulas might seem beneficial, it creates a fragile understanding. If a problem is presented in a slightly different format, or requires a conceptual leap, memorization fails to provide the necessary tools for success.
This approach hinders true problem-solving ability. Students become dependent on recognizing patterns rather than applying logical reasoning. It’s akin to knowing someone’s name and job title, but not understanding their personality or motivations. A forgotten formula, or a misremembered step, can derail the entire process.
Furthermore, memorization doesn’t build a strong foundation for future math courses. Algebraic concepts build upon each other, and a weak conceptual base will inevitably lead to difficulties down the line. Prioritize understanding over rote learning for lasting success.
Creating Your Own Algebra 1 Formula Sheet
Instead of relying on pre-made cheat sheets, actively create your own Algebra 1 formula sheet. This process isn’t just about compiling formulas; it’s a powerful learning tool. The act of writing down, organizing, and even color-coding formulas reinforces your understanding of their underlying principles.
Personalization is key. Include not just the formulas themselves, but also notes explaining why they work, and examples of how to apply them. Think of it as building a “friend profile” for each formula – understanding its nuances and how it relates to other concepts, like distribution or FOIL.
This personalized resource becomes far more valuable than a generic sheet. It reflects your individual learning style and highlights areas where you need further practice. It’s a dynamic study aid that evolves as your understanding deepens, fostering genuine mastery.
Benefits of Personalized Note-Taking
Personalized note-taking transcends simply recording information; it’s an active learning process that dramatically improves retention and comprehension. When you synthesize concepts in your own words, you force yourself to truly understand them, moving beyond mere memorization.
Creating notes tailored to your learning style – whether through visual aids, color-coding, or detailed explanations – strengthens neural pathways and makes recall easier. This is far more effective than passively copying from a textbook or relying solely on pre-made resources.
Furthermore, personalized notes become a valuable study tool, reflecting your individual struggles and triumphs. They highlight areas needing review and serve as a customized roadmap to success in Algebra 1. It’s about knowing the ‘why’ behind the formulas, like knowing a friend deeply.

Core Algebra 1 Topics
Mastering core topics – linear equations, expressions, and advanced concepts like systems of equations – is crucial for building a strong Algebra 1 foundation.
Linear Equations and Inequalities
Linear equations form the bedrock of Algebra 1, representing relationships with a constant rate of change. Understanding how to solve these equations – isolating the variable using inverse operations – is paramount. This involves mastering techniques like combining like terms and applying the distributive property.
Beyond equations, linear inequalities introduce the concept of a range of solutions, often visualized on a number line. Students must learn to graph these inequalities, paying close attention to open and closed circles, and understand how these differ from strict equality.
Furthermore, compound inequalities combine multiple inequalities, requiring students to find solutions that satisfy all conditions simultaneously. A solid grasp of these concepts is essential, as they build the foundation for more advanced algebraic manipulations and real-world problem-solving. Don’t just memorize steps; understand why they work!
Solving Linear Equations: Step-by-Step Methods
Successfully solving linear equations hinges on a systematic, step-by-step approach. Begin by simplifying both sides of the equation – distributing, and combining like terms. The core principle is to isolate the variable.
Employ inverse operations to “undo” the operations acting on the variable. If a number is added, subtract it; if multiplied, divide. Crucially, maintain balance – whatever operation is performed on one side must be mirrored on the other.
Remember, the goal isn’t just to get an answer, but to understand why each step is valid. Avoid simply memorizing procedures; focus on the underlying logic. Checking your solution by substituting it back into the original equation is a vital final step, ensuring accuracy and reinforcing conceptual understanding. Practice makes perfect!
Graphing Linear Equations: Slope-Intercept Form
The slope-intercept form, y = mx + b, is a powerful tool for visualizing linear equations. Here, ‘m’ represents the slope – the rate of change, or “rise over run” – and ‘b’ is the y-intercept, the point where the line crosses the y-axis.
To graph, start by plotting the y-intercept (0, b). Then, use the slope to find additional points. For example, a slope of 2/3 means for every 3 units you move to the right, you move 2 units up.
Understanding the relationship between the equation and the graph is key. A positive slope indicates an increasing line, while a negative slope indicates a decreasing line. Mastering this form allows for quick and accurate representation of linear relationships, fostering a deeper conceptual grasp beyond mere calculation.

Linear Inequalities and Compound Inequalities
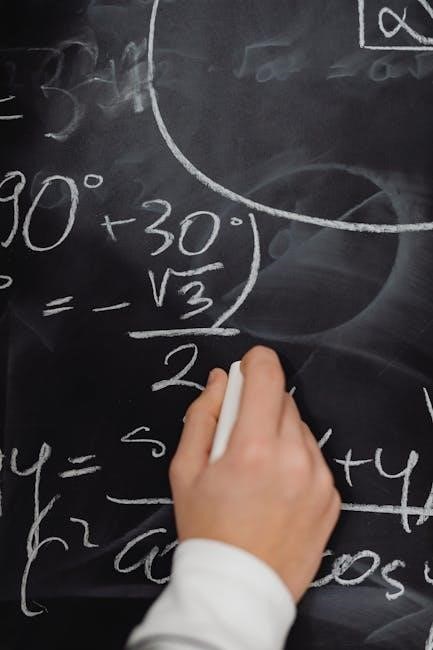
Linear inequalities, like x + 2 > 5, represent a range of solutions rather than a single value. Solving them is similar to equations, but remember to flip the inequality sign when multiplying or dividing by a negative number!
Compound inequalities combine two inequalities with “and” or “or.” “And” requires solutions satisfying both inequalities, resulting in a shared region on the number line. “Or” requires solutions satisfying either inequality, creating two separate solution sets.
Graphing these inequalities is crucial. Use open circles for “greater than” or “less than” and closed circles for “greater than or equal to” or “less than or equal to.” Visualizing the solution sets reinforces understanding and prevents common errors. Conceptual understanding is vital, avoiding simple memorization.

Expressions and Operations
Mastering algebraic manipulation requires understanding how to simplify expressions, utilizing the distributive property, and skillfully combining like terms for success.
Simplifying Algebraic Expressions
Simplifying algebraic expressions is a foundational skill in Algebra 1, moving beyond merely knowing what to do to understanding why it works. It’s not about memorizing steps, but about recognizing patterns and applying properties of operations correctly. This involves combining like terms – terms that share the same variable raised to the same power – and carefully applying the distributive property to remove parentheses.
Think of it like cleaning up a cluttered room; you’re grouping similar items together to create order. For example, 3x + 5x becomes 8x because both terms involve ‘x’. The distributive property, X(YZ) = XYZ, is crucial for expanding expressions like 2(x + 3) which simplifies to 2x + 6. Understanding how distribution relates to combining like terms and even FOIL (First, Outer, Inner, Last) builds a stronger conceptual foundation.
Avoid the trap of simply following rules without comprehension. A solid grasp of these principles will empower you to tackle more complex algebraic problems with confidence and accuracy.
The Distributive Property: A Key Concept
The distributive property, expressed as X(YZ) = XYZ, is arguably one of the most vital concepts in Algebra 1; It’s not just a rule to memorize, but a powerful tool for simplifying expressions and solving equations. It allows you to multiply a single term by two or more terms inside a set of parentheses.
Understanding why it works is key. Imagine you have 2 groups of (x + 3) items. You could find the total by first adding the items in each group (x + 3) and then multiplying by 2. Or, you could multiply 2 by x and 2 by 3 separately, then add those results (2x + 6). Both methods yield the same answer!
This property connects directly to combining like terms and the FOIL method, creating a cohesive understanding of algebraic manipulation. Mastering distribution unlocks the ability to expand expressions, solve equations, and ultimately, succeed in more advanced algebraic concepts. Don’t just apply it; internalize its logic.

Combining Like Terms: Rules and Examples
Combining like terms is a fundamental skill in algebra, built directly upon understanding the distributive property. “Like terms” are those with the same variable raised to the same power – for example, 3x and -5x are like terms, while 3x and 3x2 are not.
The rule is simple: add or subtract the coefficients (the numbers) of like terms, keeping the variable and exponent unchanged. So, 3x + (-5x) simplifies to -2x. Think of it like combining apples and oranges – you can’t directly add them, but you can combine all the apples and all the oranges separately.
This process is crucial for simplifying complex expressions. For instance, 2x + 5y ౼ x + 3y becomes (2x ౼ x) + (5y + 3y) = x + 8y. Remember, only like terms can be combined. Mastering this skill streamlines equation solving and lays the groundwork for more advanced algebraic manipulations.

Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS or BODMAS, is a cornerstone of accurate algebraic manipulation. It dictates the sequence in which calculations must be performed to arrive at the correct solution. PEMDAS stands for Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
BODMAS is a British equivalent: Brackets, Orders (powers and square roots), Division and Multiplication, Addition and Subtraction. Regardless of the acronym, the principle remains consistent. Failing to adhere to this order leads to incorrect results.
For example, in the expression 2 + 3 * 4, multiplication must be done before addition. Therefore, 3 * 4 = 12, and then 2 + 12 = 14. Ignoring this order and adding first (2+3=5, then 5*4=20) yields a wrong answer. Consistent application of PEMDAS/BODMAS is vital for simplifying expressions and solving equations accurately.

Advanced Algebra 1 Concepts
Mastering systems of equations, factoring, and quadratic equations builds upon foundational skills, preparing students for more complex mathematical challenges ahead.
Systems of Equations: Solving Methods
Understanding how to solve systems of equations is crucial in Algebra 1, representing real-world scenarios where multiple variables interact. Several methods exist, each with its strengths. Substitution involves solving one equation for a variable and plugging that expression into the other equation, reducing it to a single variable problem.
Elimination (or addition) focuses on manipulating the equations to have opposite coefficients for one variable, allowing you to add the equations together and eliminate that variable. Graphing provides a visual representation; the solution is the point where the lines intersect.
Choosing the best method depends on the specific system. Substitution is effective when one equation is easily solved for a variable. Elimination shines when coefficients are easily manipulated. A solid grasp of these techniques is essential for tackling more advanced algebraic problems later on, and building a strong foundation in problem-solving.
Factoring Polynomials: Techniques and Strategies
Factoring polynomials is a fundamental skill in Algebra 1, serving as a building block for solving equations and simplifying expressions. It’s essentially the reverse of distribution, breaking down a polynomial into a product of simpler factors. Common techniques include Greatest Common Factor (GCF) factoring, where you identify the largest factor shared by all terms.
Difference of Squares applies to expressions like a2 ー b2, factoring into (a + b)(a ౼ b). Trinomial factoring involves finding two numbers that add up to the middle coefficient and multiply to the constant term. Recognizing patterns and practicing consistently are key to mastering these techniques.
Remember, understanding why factoring works – its connection to the distributive property – is more valuable than simply memorizing steps. A well-constructed formula sheet can aid recall, but conceptual understanding is paramount for success.
Quadratic equations, those with a highest power of x equal to 2, represent a significant step in Algebra 1. They often appear in the form ax2 + bx + c = 0, and solving them involves finding the values of ‘x’ that satisfy the equation. Several methods exist for finding these solutions, also known as roots or zeros.
Factoring, when applicable, is a straightforward approach. The quadratic formula, x = [-b ± √(b2 ౼ 4ac)] / 2a, provides a solution for any quadratic equation, regardless of factorability. Completing the square is another technique, though often more complex.
Just like with other concepts, avoid mere memorization. Understand why the quadratic formula works and when each method is most efficient. Building a personalized formula sheet can be incredibly helpful for quick reference during problem-solving.
Exponents and Polynomials: Rules and Applications
Exponents and polynomials form a foundational pillar of algebra, demanding a firm grasp of their underlying rules. Key exponent rules include product of powers (xm * xn = xm+n), quotient of powers (xm / xn = xm-n), power of a power ((xm)n = xmn), and zero exponent (x0 = 1).
Polynomials, expressions with multiple terms involving variables raised to non-negative integer powers, require understanding of addition, subtraction, multiplication, and sometimes division. The distributive property is crucial for simplifying and expanding polynomial expressions.
Don’t simply memorize rules; strive to understand why they work. Relate exponent rules to the concept of repeated multiplication. A well-organized, personalized notes PDF, perhaps color-coded, will aid in mastering these essential algebraic tools.
